Chuyên đề về BIT (Binary Index Tree)
Binary Indexed Tree còn gọi là Fenwick Tree cung cấp 1 cách để biểu diễn 1 mảng các số trong 1 mảng, cho phép tổng tiền tố được tính một cách hiệu quả. Ví dụ, 1 mảng [2,3,-1,0,6] được cho, thì tổng tiền tố của 3 phần tử đầu tiên [2,3,-1] là 2+3+(-1)=4. Tính tổng tiền tố một cách hiệu quả là hữu ích trong nhiều hoàn cảnh. Chúng ta hãy bắt đầu với 1 ví dụ đơn giản.
Cho 1 mảng a[], và 2 loại phép toán được biểu diễn trên nó.
1. Thay đổi giá trị được lưu tại chỉ số i. (Cái này được gọi là phép toán update điểm).
2. Tìm tổng một tổng của 1 tiền tố có độ dài là k (Cái này được gọi là truy vấn range sum).
Một cách tiếp cận theo kiểu implement là:
```
Đây là một giải pháp tốt, tuy nhiên không may mắn thay, thời gian cần thiết để tính tổng tiền tố tỷ lệ thuận với độ dài của mảng, do đó, điều này thường sẽ hết thời gian khi một số lượng lớn các hoạt động xen kẻ như vậy được thực hiện.
Một giải pháp hiệu quả là sử dụng cây phân đoạn (Segment Tree) có thể thực hiện cả hai thao tác trong O(logN) thời gian.
Việc sử dụng BIT cũng vậy, chúng ta có thể biểu diễn cả hai nhiệm vụ trong thời gian O(logN). Nhưng tại sao phải tìm hiểu cấu trúc dữ liệu khác khi Segment Tree có thể làm việc này cho chúng ta, Nó có ý nghĩa là vì BIT yêu cầu ít space hơn, và chúng dễ implement trong các cuộc thi lập trình. (Tổng các dòng code không quá 8-10 dòng).
Trước khi bắt đầu với BIT, chúng ta cần có một cái nhìn cụ thể về biến đổi bit một chút
Giả sử ta có số x=1110 (Được viết dưới dạng nhị phân).
Ta chú ý một điều sau: Phép toán x&(-x) sẽ trả lại một kết quả chính là bit 1 từ phải quá trái đầu tiên được giữ nguyên, còn các bit khác đều bị clear.
Chứng minh:
Giả sử: x=a1b (dạng nhị phân), ở đây a là một chuỗi nhị phân gồm các số 1 và 0 có độ dài bất kỳ, và b cũng là 1 chuỗi nhị phân bất kỳ nhưng chỉ toàn số 0.
Khi đó ta có: -x = (a1b)'+1=a'0b'+1=a'0(0...0)'+1=a'0(111..11)+1=a'1(000..0)=a'1b.
Do đó x&(-x)=(00...000)1(00..000)
Ví dụ: x=10(in decimal ) = 1010 (in binary).
Khi đó bit cuối cùng được set là ; x&(-x)=(10)1(0)&(01)1(0)=0010=2 (in decimal).
Một cách dễ hiểu hơn đó là Ta viết 10=2^p.q (trong đó q lẻ). Khi đó p chính là giá trị của x&(-x).
Bây giờ, chúng ta sẽ đi sâu vào BIT.
Chúng ta biết rằng, mỗi số nguyên luôn có thể biểu diễn được thành tổng các lũy thừa của 2. Tương tự, cho một mảng có kích thước N, chúng ta có thể duy trì mảng BIT[] thỏa mãn, bất kì index nào chúng ta có thể lưu tổng của một vài số khác của mảng đã cho. Cái này còn được gọi là partial sum tree.
Chúng ta hãy sử dụng ví dụ để hiểu BIT[] lưu trữ như thế nào.
```
```
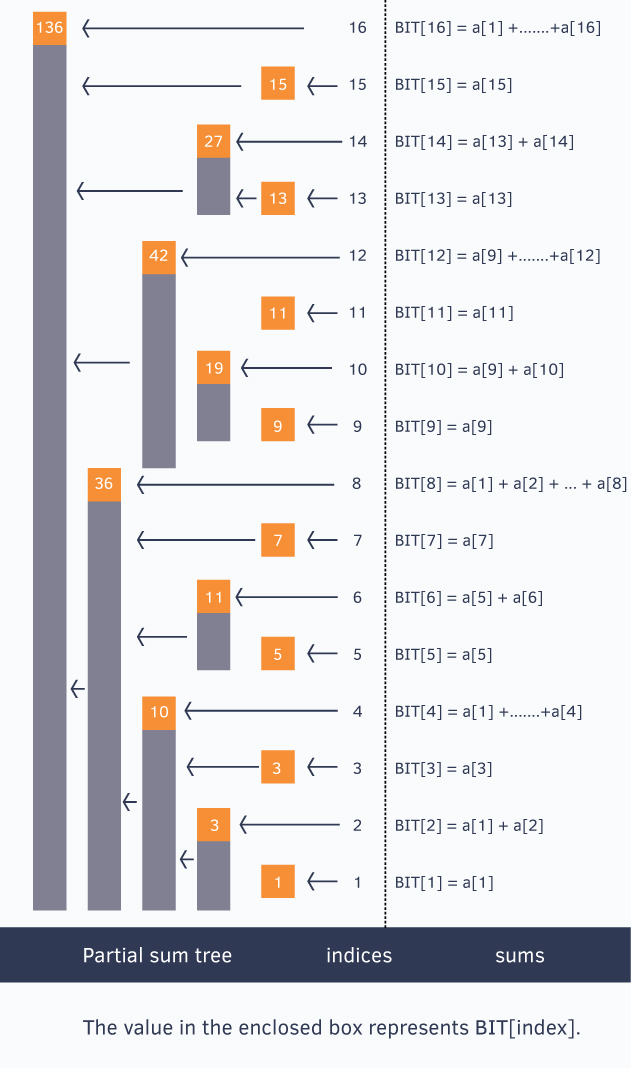
Ta có một chú ý như sau: Giả sử i=2^k.p ( với p là số lẻ), thì ta có; BIT[i]=a[i-2^k+1]+...+a[i]
Cụ thể: Giả sử i=15. Ta có 15=2^0.15. Nên BIT[15]=a[15].
hoặc giả sử ta lấy i=12. Ta có: 12=2^2.3/ Do đó BIT[12]=a[9]+a[10]+..+a[12].
Ta có một điều chú ý: BIT[x]=a[x] nếu x lẻ, và BIT[x]=a[1]+...a[x] nếu x là lũy thừa của 2.
Bây giờ chúng ta hãy xem cách xây dựng cây này và sau đó chúng ta sẽ đến truy vấn của cây với các tổng tiền tố. BIT[] là một mảng có kích thước =1+kích thước của mảng đã cho , nơi mà chúng ta có thể biểu diễn những phép toán. Khởi tạo tất cả những giá trị trong mảng BIT[] bằng 0. Sau đó chúng ta gọi hàm update() với mỗi phần tử của mảng được cho để dựng BIT. Toán tử update() được thảo luận dưới đây.
```
Okay, nếu bạn chưa hiểu hàm update() trên hoạt động như thế nào. Hãy lấy 1 ví dụ và thử hiểu chúng.
Giả sử ta gọi update(13,2).
Ở đây, chúng ta thấy chỉ số 13,14 và 16 sẽ được chạy dần lên từ chỉ số 13 và vì vậy chúng ta cần cộng 2 vào chúng.
Khởi tạo x=13, chúng ta update BIT[13].
```
Tiếp theo x+=x&(-x)
Lệnh này có ý nghĩa ta cộng thêm 1 vào bit 1 bên phải nhất của x.
Ta có x=13(1101), khi cộng thêm 1 vào bit bên phải nhất thì x=13+1=14, chúng ta update BIT[14].
```
Bây giờ 14 là 1110, tiếp tục ta cộng 1 vào bit 1 bên phải nhất của x, khi đó x trở thành 14+2=16(10000). Chúng ta update BIT[16].
```
Bằng cách này, khi một thao tác update() được thực hiện trên chỉ số x thì nó sẽ update hết tất cả những chỉ số của BIT[] mà bao trùm lên x và vẫn duy trì được mảng BIT[].
Nếu chúng ta nhìn vào vòng lặp for của phép toán update(), chúng ta có thể thấy rằng độ phức tạp ở trên chỉ có O(logN).
Tiếp theo là làm thế nào để chúng ta truy vấn cấu trúc dữ liệu này cho tổng tiền tố? Hãy nhìn vào phép toán truy vấn.
```
Hàm query ở trên sẽ trả về tổng của x phần tử đầu tiên của mảng được cho. . Quy trình ví dụ các bạn có thể xem tại đây: https://www.hackerearth.com/practice/data-structures/advanced-data-structures/fenwick-binary-indexed-trees/tutorial/
Ở đây là toàn bộ chương trình:
```
Khi nào thì sử dụng BIT ?
Trước khi sử dụng BIT để thực hiện phép toán, điều đầu tiên chúng ta cần phải xác nhận rằng phép toán hoặc hàm phải kết nối với nhau:
Nghĩa là f(f(a,b),c)=f(a,f(b,c)), điều này đúng với seg-tree.
Cho 1 mảng a[], và 2 loại phép toán được biểu diễn trên nó.
1. Thay đổi giá trị được lưu tại chỉ số i. (Cái này được gọi là phép toán update điểm).
2. Tìm tổng một tổng của 1 tiền tố có độ dài là k (Cái này được gọi là truy vấn range sum).
Một cách tiếp cận theo kiểu implement là:
```
int a[] = {2, 1, 4, 6, -1, 5, -32, 0, 1};
void update(int i, int v) //assigns value v to a[i]
{
a[i] = v;
}
int prefixsum(int k) //calculate the sum of all a[i] such that 0 <= i < k
{
int sum = 0;
for(int i = 0; i < k; i++)
sum += a[i];
return sum;
}Đây là một giải pháp tốt, tuy nhiên không may mắn thay, thời gian cần thiết để tính tổng tiền tố tỷ lệ thuận với độ dài của mảng, do đó, điều này thường sẽ hết thời gian khi một số lượng lớn các hoạt động xen kẻ như vậy được thực hiện.
Một giải pháp hiệu quả là sử dụng cây phân đoạn (Segment Tree) có thể thực hiện cả hai thao tác trong O(logN) thời gian.
Việc sử dụng BIT cũng vậy, chúng ta có thể biểu diễn cả hai nhiệm vụ trong thời gian O(logN). Nhưng tại sao phải tìm hiểu cấu trúc dữ liệu khác khi Segment Tree có thể làm việc này cho chúng ta, Nó có ý nghĩa là vì BIT yêu cầu ít space hơn, và chúng dễ implement trong các cuộc thi lập trình. (Tổng các dòng code không quá 8-10 dòng).
Trước khi bắt đầu với BIT, chúng ta cần có một cái nhìn cụ thể về biến đổi bit một chút
Giả sử ta có số x=1110 (Được viết dưới dạng nhị phân).
Ta chú ý một điều sau: Phép toán x&(-x) sẽ trả lại một kết quả chính là bit 1 từ phải quá trái đầu tiên được giữ nguyên, còn các bit khác đều bị clear.
Chứng minh:
Giả sử: x=a1b (dạng nhị phân), ở đây a là một chuỗi nhị phân gồm các số 1 và 0 có độ dài bất kỳ, và b cũng là 1 chuỗi nhị phân bất kỳ nhưng chỉ toàn số 0.
Khi đó ta có: -x = (a1b)'+1=a'0b'+1=a'0(0...0)'+1=a'0(111..11)+1=a'1(000..0)=a'1b.
Do đó x&(-x)=(00...000)1(00..000)
Ví dụ: x=10(in decimal ) = 1010 (in binary).
Khi đó bit cuối cùng được set là ; x&(-x)=(10)1(0)&(01)1(0)=0010=2 (in decimal).
Một cách dễ hiểu hơn đó là Ta viết 10=2^p.q (trong đó q lẻ). Khi đó p chính là giá trị của x&(-x).
Bây giờ, chúng ta sẽ đi sâu vào BIT.
Chúng ta biết rằng, mỗi số nguyên luôn có thể biểu diễn được thành tổng các lũy thừa của 2. Tương tự, cho một mảng có kích thước N, chúng ta có thể duy trì mảng BIT[] thỏa mãn, bất kì index nào chúng ta có thể lưu tổng của một vài số khác của mảng đã cho. Cái này còn được gọi là partial sum tree.
Chúng ta hãy sử dụng ví dụ để hiểu BIT[] lưu trữ như thế nào.
```
//for ease, we make sure our given array is 1-based indexed
int a[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
```
Ta có một chú ý như sau: Giả sử i=2^k.p ( với p là số lẻ), thì ta có; BIT[i]=a[i-2^k+1]+...+a[i]
Cụ thể: Giả sử i=15. Ta có 15=2^0.15. Nên BIT[15]=a[15].
hoặc giả sử ta lấy i=12. Ta có: 12=2^2.3/ Do đó BIT[12]=a[9]+a[10]+..+a[12].
Ta có một điều chú ý: BIT[x]=a[x] nếu x lẻ, và BIT[x]=a[1]+...a[x] nếu x là lũy thừa của 2.
Bây giờ chúng ta hãy xem cách xây dựng cây này và sau đó chúng ta sẽ đến truy vấn của cây với các tổng tiền tố. BIT[] là một mảng có kích thước =1+kích thước của mảng đã cho , nơi mà chúng ta có thể biểu diễn những phép toán. Khởi tạo tất cả những giá trị trong mảng BIT[] bằng 0. Sau đó chúng ta gọi hàm update() với mỗi phần tử của mảng được cho để dựng BIT. Toán tử update() được thảo luận dưới đây.
```
void update(int x, int val) //add "val" at index "x"
{
for(; x <= n; x += x&-x)
BIT[x] += val;
}Okay, nếu bạn chưa hiểu hàm update() trên hoạt động như thế nào. Hãy lấy 1 ví dụ và thử hiểu chúng.
Giả sử ta gọi update(13,2).
Ở đây, chúng ta thấy chỉ số 13,14 và 16 sẽ được chạy dần lên từ chỉ số 13 và vì vậy chúng ta cần cộng 2 vào chúng.
Khởi tạo x=13, chúng ta update BIT[13].
```
BIT[13] += 2;Tiếp theo x+=x&(-x)
Lệnh này có ý nghĩa ta cộng thêm 1 vào bit 1 bên phải nhất của x.
Ta có x=13(1101), khi cộng thêm 1 vào bit bên phải nhất thì x=13+1=14, chúng ta update BIT[14].
```
BIT[14] += 2;Bây giờ 14 là 1110, tiếp tục ta cộng 1 vào bit 1 bên phải nhất của x, khi đó x trở thành 14+2=16(10000). Chúng ta update BIT[16].
```
BIT[16] += 2;Bằng cách này, khi một thao tác update() được thực hiện trên chỉ số x thì nó sẽ update hết tất cả những chỉ số của BIT[] mà bao trùm lên x và vẫn duy trì được mảng BIT[].
Nếu chúng ta nhìn vào vòng lặp for của phép toán update(), chúng ta có thể thấy rằng độ phức tạp ở trên chỉ có O(logN).
Tiếp theo là làm thế nào để chúng ta truy vấn cấu trúc dữ liệu này cho tổng tiền tố? Hãy nhìn vào phép toán truy vấn.
```
int query(int x) //returns the sum of first x elements in given array a[]
{
int sum = 0;
for(; x > 0; x -= x&-x)
sum += BIT[x];
return sum;
}Hàm query ở trên sẽ trả về tổng của x phần tử đầu tiên của mảng được cho. . Quy trình ví dụ các bạn có thể xem tại đây: https://www.hackerearth.com/practice/data-structures/advanced-data-structures/fenwick-binary-indexed-trees/tutorial/
Ở đây là toàn bộ chương trình:
```
int BIT[1000], a[1000], n;
void update(int x, int val)
{
for(; x <= n; x += x&-x)
BIT[x] += val;
}
int query(int x)
{
int sum = 0;
for(; x > 0; x -= x&-x)
sum += BIT[x];
return sum;
}
int main()
{
scanf(“%d”, &n);
int i;
for(i = 1; i <= n; i++)
{
scanf(“%d”, &a[i]);
update(i, a[i]);
}
printf(“sum of first 10 elements is %d\n”, query(10));
printf(“sum of all elements in range [2, 7] is %d\n”, query(7) – query(2-1));
return 0;
}Khi nào thì sử dụng BIT ?
Trước khi sử dụng BIT để thực hiện phép toán, điều đầu tiên chúng ta cần phải xác nhận rằng phép toán hoặc hàm phải kết nối với nhau:
Nghĩa là f(f(a,b),c)=f(a,f(b,c)), điều này đúng với seg-tree.
Nhận xét
Đăng nhận xét